Data Science - Statistics Correlation vs. Causality
Correlation Does Not Imply Causality
Correlation measures the numerical relationship between two variables.
A high correlation coefficient (close to 1), does not mean that we can for sure conclude an actual relationship between two variables.
A classic example:
- During the summer, the sale of ice cream at a beach increases
- Simultaneously, drowning accidents also increase as well
Does this mean that increase of ice cream sale is a direct cause of increased drowning accidents?
The Beach Example in Python
Here, we constructed a fictional data set for you to try:
Example
import pandas as pd
import matplotlib.pyplot as plt
Drowning_Accident = [20,40,60,80,100,120,140,160,180,200]
Ice_Cream_Sale =
[20,40,60,80,100,120,140,160,180,200]
Drowning = {"Drowning_Accident":
[20,40,60,80,100,120,140,160,180,200],
"Ice_Cream_Sale":
[20,40,60,80,100,120,140,160,180,200]}
Drowning = pd.DataFrame(data=Drowning)
Drowning.plot(x="Ice_Cream_Sale", y="Drowning_Accident", kind="scatter")
plt.show()
correlation_beach = Drowning.corr()
print(correlation_beach)
Try it Yourself »
Output:
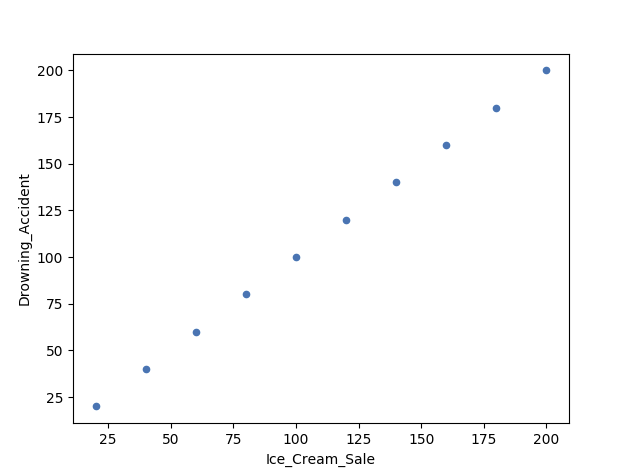
Correlation vs Causality - The Beach Example
In other words: can we use ice cream sale to predict drowning accidents?
The answer is - Probably not.
It is likely that these two variables are accidentally correlating with each other.
What causes drowning then?
- Unskilled swimmers
- Waves
- Cramp
- Seizure disorders
- Lack of supervision
- Alcohol (mis)use
- etc.
Let us reverse the argument:
Does a low correlation coefficient (close to zero) mean that change in x does not affect y?
Back to the question:
- Can we conclude that Average_Pulse does not affect Calorie_Burnage because of a low correlation coefficient?
The answer is no.
There is an important difference between correlation and causality:
- Correlation is a number that measures how closely the data are related
- Causality is the conclusion that x causes y.
Tip: Always critically reflect over the concept of causality when doing predictions!


